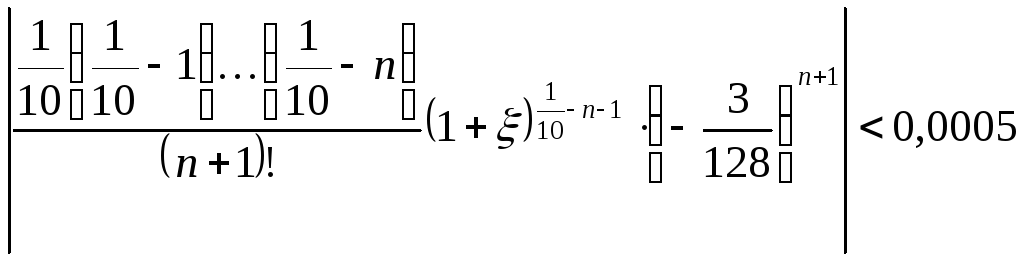Остаточный член формулы Тейлора в форме Лагранжа
Единая коллекция Цифровых образовательных ресурсов Искать в текущем разделе. Например: предлоги. Расширенный поиск. Тематический рубрикатор рубрикатор хранилища. Школьный математический словарь-справочник. Поддержка ресурса.










Чтобы найти первую производную в нуле, нам придётся воспользоваться определением — просто так применить стандартные правила дифференцирования не получится, так как функция по-разному опрделена в нуле и вне нуля. Дальше можно продолжать в том же духе. Каждый раз будет получаться 0. Докажите, что это действительно так! Итак, мы получаем, что все производные f в нуле равны нулю.




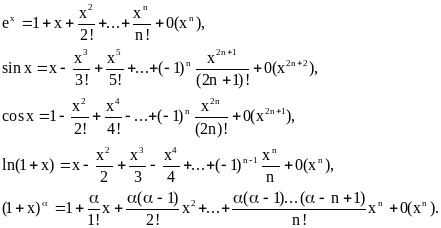
Разложим в качестве примера функцию в ряд Тейлора Маклорена в точке. Вычислим значение , ограничимся , более точное значение с округлением до целых Как видно наша абсолютная погрешность приближения в точке равна , при. Теперь обратим задачу, найдём число , при котором в точке функции абсолютная погрешность будет заметим что входит в данный диапазон.